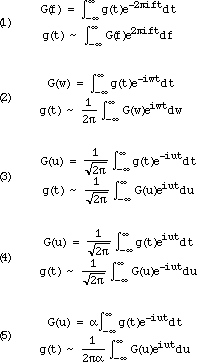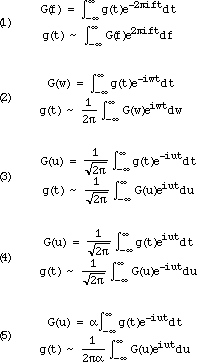分数次フーリエ変換

数学の調和解析の分野において、分数次フーリエ変換（分数階フーリエ変換とも、英: fractional Fourier transform, FRFT）とは、フーリエ変換を一般化した一群の線形変換をいい、フーリエ変換の次数が整数でなくなったものと考えることができる。従って、関数を時間領域と周波数領域の「中間」領域に変換することができる。FRFTは、フィルター設計や信号解析、位相回復やパターン認識などに応用される。

FRFTは、分数次の畳み込み、相関関数、その他の操作の定義に使うことができ、さらに線形正準変換へと一般化できる。 FRFTの初期の定義はエドワード・コンドンにより導入された。この定義は位相空間における回転のグリーン関数を解くことによるものだった。また、ウィーナーのエルミート多項式についての仕事を一般化することによる、ナミアスにより導入された定義も存在する。

しかし、信号処理の分野において広く認知されるようになったのは、1993年前後にいくつかのグループにより独立に再導入されてからであった。その時から、分数次フーリエ領域に帯域制限された信号にシャノンの標本化定理を拡張するという興味が巻き起こった。

全く異なる「分数次フーリエ変換」の意味がベイリーとシュヴァルツトラウバーにより、本質的にはz変換の別名として、特に離散フーリエ変換を周波数空間で分数量だけシフトして（入力に線形チャープを乗じて）一部の周波数点（スペクトルの一部分だけ）において評価したものに相当する変換を指す用語として導入された（このような変換はブルーシュタインのFFTアルゴリズムにより効率的に評価することができる）。しかし、この用語はほとんどの技術的文献では使われなくなり、FRFTに取ってかわられた。以降ではFRFTについて説明する。

導入

関数 ƒ: R → C に対する連続フーリエ変換 ${\displaystyle {\mathcal {F}}}$ は L² 上のユニタリ作用素であり、関数 ƒ をその周波数版 ˆƒ̂ に変換する。

${\displaystyle {\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-2\pi ix\xi }\,\mathrm {d} x}$  ここで ξ は全ての実数とする。

逆に、ƒ は ˆƒ̂ から逆変換 ${\displaystyle {\mathcal {F}}^{-1}}$ により得られる。

${\displaystyle f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )\ e^{2\pi i\xi x}\,\mathrm {d} \xi ,}$   ここで x は全ての実数とする。

ここで、n 回反復された ${\displaystyle {\mathcal {F}}^{n}}$ を ${\displaystyle {\mathcal {F}}^{n}[f]={\mathcal {F}}[{\mathcal {F}}^{n-1}[f]]}$、n が非負整数のとき ${\displaystyle {\mathcal {F}}^{-n}=({\mathcal {F}}^{-1})^{n}}$、および ${\displaystyle {\mathcal {F}}^{0}[f]=f}$ により定義し、考察することとする。${\displaystyle {\mathcal {F}}}$ は周期4の自己同型、つまり全ての関数 ƒ について ${\displaystyle {\mathcal {F}}^{4}[f]=f}$ であるから、この列は有限である。

より正確には、時間を反転させるパリティ作用素 ${\displaystyle {\mathcal {P}}[f]\colon t\mapsto f(-t)}$ を導入すると、次の性質が成り立つ。

${\displaystyle {\mathcal {F}}^{0}=\mathrm {Id} ,\qquad {\mathcal {F}}^{1}={\mathcal {F}},\qquad {\mathcal {F}}^{2}={\mathcal {P}},\qquad {\mathcal {F}}^{4}=\mathrm {Id} }$

${\displaystyle {\mathcal {F}}^{3}={\mathcal {F}}^{-1}={\mathcal {P}}\circ {\mathcal {F}}={\mathcal {F}}\circ {\mathcal {P}}}$

FrFTは、ここに定義される一連の線形変換をさらに拡張し、フーリエ変換の非整数次 n = 2α/π 次の羃を扱えるようにするものである。

定義

任意の実数 α に対して、関数 ƒ の α-角分数次フーリエ変換を ${\displaystyle {\mathcal {F}}_{\alpha }(u)}$ と表記することにし、次のように定義する。

（平方根は結果の引数が区間 ${\displaystyle [-\pi /2,\pi /2]}$ となるように定義する。）

α が π の整数倍のとき、上式の余接関数と余割関数は発散するが、極限を取ることによりこれを扱うことができ、結果として非積分関数にディラックのデルタ関数が表われる。より直接的には、 ${\displaystyle {\mathcal {F}}^{2}(f)=f(-t)}$ であるから、 ${\displaystyle {\mathcal {F}}_{\alpha }(f)}$ は α が π の偶数倍または奇数倍のとき、それぞれ f(t) または f(−t) を与える。

α = π/2 のとき、これは連続フーリエ変換の定義と一致し、α = −π/2 の場合は連続フーリエ逆変換の定義と一致する。

FRFT後の関数の引数 u は空間的な引数 x でも周波数的な引数 ξ でもない。これをこれら二つの座標 (x,ξ) の線形結合と考えることができる理由を見ていこう。α-角分数領域を区別するために、x_a を ${\displaystyle {\mathcal {F}}_{\alpha }}$ の引数とすることにする。

備考: 周波数ではなく角周波数 ω を使うコンベンションでは、FrFT 公式はメーラー核となる。

${\displaystyle {\mathcal {F}}_{\alpha }(f)(\omega )={\sqrt {\frac {1-i\cot(\alpha )}{2\pi }}}e^{i\cot(\alpha )\omega ^{2}/2}\int _{-\infty }^{\infty }e^{-i\csc(\alpha )\omega t i\cot(\alpha )t^{2}/2}f(t)\,dt~.}$

性質

α-次の分数次フーリエ変換演算子 ${\displaystyle {\mathcal {F}}_{\alpha }}$ は次のような性質を持つ。

• 加法性: 任意の実数角 α, β について、

${\displaystyle {\mathcal {F}}_{\alpha \beta }={\mathcal {F}}_{\alpha }\circ {\mathcal {F}}_{\beta }={\mathcal {F}}_{\beta }\circ {\mathcal {F}}_{\alpha }}$

• 線形性:

${\displaystyle {\mathcal {F}}_{\alpha }\left[\sum \nolimits _{k}b_{k}f_{k}(u)\right]=\sum \nolimits _{k}b_{k}{\mathcal {F}}_{\alpha }\left[f_{k}(u)\right]}$

• 整数次: α が ${\displaystyle \pi /2}$ の整数倍のとき、

${\displaystyle {\mathcal {F}}_{\alpha }={\mathcal {F}}_{\frac {k\pi }{2}}={\mathcal {F}}^{k}=({\mathcal {F}})^{k}}$

さらに言えば、次のような関係もある。

${\displaystyle {\begin{aligned}{\mathcal {F}}^{2}&={\mathcal {P}}&&{\mathcal {P}}[f(u)]=f(-u)\\{\mathcal {F}}^{3}&={\mathcal {F}}^{-1}=({\mathcal {F}})^{-1}\\{\mathcal {F}}^{4}&={\mathcal {F}}^{0}={\mathcal {I}}\\{\mathcal {F}}^{i}&={\mathcal {F}}^{j}&&i\equiv j\mod 4\end{aligned}}}$

• 逆変換:

${\displaystyle ({\mathcal {F}}_{\alpha })^{-1}={\mathcal {F}}_{-\alpha }}$

• 可換性:

${\displaystyle {\mathcal {F}}_{\alpha _{1}}{\mathcal {F}}_{\alpha _{2}}={\mathcal {F}}_{\alpha _{2}}{\mathcal {F}}_{\alpha _{1}}}$

• 結合法則

${\displaystyle \left({\mathcal {F}}_{\alpha _{1}}{\mathcal {F}}_{\alpha _{2}}\right){\mathcal {F}}_{\alpha _{3}}={\mathcal {F}}_{\alpha _{1}}\left({\mathcal {F}}_{\alpha _{2}}{\mathcal {F}}_{\alpha _{3}}\right)}$

• パーセバルの定理:

${\displaystyle \int f^{*}(u)g(u)du=\int f_{\alpha }^{*}(u)g_{\alpha }(u)du}$

この性質はユニタリ性と類似している。エネルギーもしくはノルム保存が特殊例である。

• 時間反転:

${\displaystyle {\mathcal {F}}_{\alpha }{\mathcal {P}}={\mathcal {P}}{\mathcal {F}}_{\alpha }}$

${\displaystyle {\mathcal {F}}_{\alpha }[f(-u)]=f_{\alpha }(-u)}$

• シフトされた関数の変換:

シフト演算子と位相シフト演算子をそれぞれ以下のように定義する。

${\displaystyle {\mathcal {SH}}(u_{0})[f(u)]=f(u u_{0})}$

${\displaystyle {\mathcal {PH}}(v_{0})[f(u)]=e^{j2\pi v_{0}u}f(u)}$

すると、

${\displaystyle {\begin{aligned}{\mathcal {F}}_{\alpha }{\mathcal {SH}}(u_{0})&=e^{j\pi u_{0}^{2}\sin \alpha \cos \alpha }{\mathcal {PH}}(u_{0}\sin \alpha ){\mathcal {SH}}(u_{0}\cos \alpha )F_{\alpha }\\{\mathcal {F}}_{\alpha }[f(u u_{0})]&=e^{j\pi u_{0}^{2}\sin \alpha \cos \alpha }e^{j2\pi uu_{0}\sin \alpha }f_{\alpha }(u u_{0}\cos \alpha )\end{aligned}}}$

• スケールされた関数の変換

スケーリング演算子およびチャープ乗算演算子以下のように定義する。

${\displaystyle M(M)[f(u)]=|M|^{-{\frac {1}{2}}}f\left({\tfrac {u}{M}}\right)}$

${\displaystyle Q(q)[f(u)]=e^{-j\pi qu^{2}}f(u)}$

すると、以下が成り立つ。

${\displaystyle {\begin{aligned}{\mathcal {F}}_{\alpha }M(M)&=Q\left(-\cot \left({\frac {1-\cos ^{2}\alpha '}{\cos ^{2}\alpha }}\alpha \right)\right)\times M\left({\frac {\sin \alpha }{M\sin \alpha '}}\right){\mathcal {F}}_{\alpha '}\\[6pt]{\mathcal {F}}_{\alpha }\left[|M|^{-{\frac {1}{2}}}f\left({\tfrac {u}{M}}\right)\right]&={\sqrt {\frac {1-j\cot \alpha }{1-jM^{2}\cot \alpha }}}e^{j\pi u^{2}\cot \left({\frac {1-\cos ^{2}\alpha '}{\cos ^{2}\alpha }}\alpha \right)}\times f_{a}\left({\frac {Mu\sin \alpha '}{\sin \alpha }}\right)\end{aligned}}}$

${\displaystyle f(u/M)}$ の分数次フーリエ変換は ${\displaystyle f_{\alpha }(u)}$ をスケールしたものにはならないということに注意が必要である。むしろ、 α ≠ α′ のときは ${\displaystyle f(u/M)}$ の分数次フーリエ変換は ${\displaystyle f_{\alpha }'(u)}$ をスケールおよびチャープ変調したものになる。

分数次核関数

FrFTは次のように積分変換として表わせる。

${\displaystyle {\mathcal {F}}_{\alpha }f(u)=\int K_{\alpha }(u,x)f(x)\,\mathrm {d} x}$

ここで、α-角核関数はつぎのようになる。

${\displaystyle K_{\alpha }(u,x)={\begin{cases}{\sqrt {1-i\cot(\alpha )}}\exp \left(i\pi (\cot(\alpha )(x^{2} u^{2})-2\csc(\alpha )ux)\right)&{\mbox{if }}\alpha {\mbox{ is not a multiple of }}\pi ,\\\delta (u-x)&{\mbox{if }}\alpha {\mbox{ is a multiple of }}2\pi ,\\\delta (u x)&{\mbox{if }}\alpha \pi {\mbox{ is a multiple of }}2\pi ,\\\end{cases}}}$

（二乗根は偏角が区間 ${\displaystyle [-\pi /2,\pi /2]}$ に収まるように定義するものとする）

ここでも、特殊な場合は α が π の整数倍に近付いたときの挙動と矛盾なく定義されている。

FrFTは、核関数と同じ次のような性質を持つ。

• 対称性: ${\displaystyle K_{\alpha }(u,u')=K_{\alpha }(u',u)}$
• 逆関数: ${\displaystyle K_{\alpha }^{-1}(u,u')=K_{\alpha }^{*}(u,u')=K_{-\alpha }(u',u)}$
• 加法性: ${\displaystyle K_{\alpha \beta }(u,u')=\int K_{\alpha }(u,u'')K_{\beta }(u'',u')\,\mathrm {d} u''.}$

関連する変換

離散フーリエ変換のような類似の変換にも、分数次フーリエ変換と関連する分数次への一般化が存在する。離散分数次フーリエ変換は、Zeev Zalevsky による定義が、(Candan, Kutay & Ozaktas 2000) および (Ozaktas, Zalevsky & Kutay 2001, Chapter 6) に見える。

分数次ウェーブレット変換 (FRWT): 古典的ウェーブレット変換 (WT) の分数次フーリエ変換 (FRFT) 領域への一般化。FRWT は WT および FRFT の制限を改善するために提案された。この変換は WT からマルチ解像度解析の利点を受け継ぐだけでなく、FRFT と類似の分数次領域での信号の表現力をあわせもつ。既存の FRWT に比べて、Shi, Zhang, Liu により2012年に定義された FRWT は時間・周波数混合平面における信号表現力がある。

関連するフーリエ変換の一般化について、チャープレット変換も参照されたい。

一般化

フーリエ変換は本質的にボソン的である。これがうまくいくのは重ね合わせの原理との整合性のためであり、干渉パターンと関連がある。対して、フェルミオン的フーリエ変換も存在する。これらは超対称 FRFT および超対称ラドン変換に一般化できる。分数次ラドン変換、シンプレクティック FRFT、シンプレクティックウェーブレット変換も存在する。量子回路はユニタリ操作に基いているため、後者が関数空間上のユニタリ作用素である積分変換の計算に有用である。FRFTを実装する量子回路も設計されている。

分数次フーリエ変換の解釈

フーリエ変換の通常の解釈は、時間領域信号を周波数領域信号へと変換するものである。これに対して、逆フーリエ変換の解釈は周波数領域信号を時間領域信号に変換するものである。見て分かるように、分数次フーリエ変換は（時間領域でも周波数領域でもどちらでもよい）信号を時間と周波数の間の領域の信号へと変換するもの、つまり時間・周波数領域での回転と解釈できる。この見方は線形正準変換により一般化される。この変換は、分数次フーリエ変換を一般化し、時間・周波数領域における回転以外の線形変換を可能とする。

下の図を例にとろう。時間領域信号が（下のとおり）矩形の場合、周波数領域ではsinc関数となる。しかし、分数次フーリエ変換を作用させた場合、矩形信号は時間と周波数の間の領域の信号が得られる。

実際、分数次フーリエ変換は時間周波数分布上の回転操作である。上述の定義から、α = 0 の場合の分数次フーリエ変換では何も変化せず、α = π/2 の場合はフーリエ変換となり、時間周波数分布を π/2 だけ回転させる。α がその他の値の場合、分数次フーリエ変換は時間周波数分布を α だけ回転させる。次の図はさまざまな α の値における分数次フーリエ変換の結果である。

応用

分数次フーリエ変換は時間周波数解析や DSP に用いられることがある。ノイズのフィルタリングにも有用だが、ノイズと信号が時間・周波数領域において重ならないことが条件となる。次の例を考えよう。ノイズを除去したいが直接フィルタを適用することができない場合、まず分数次フーリエ変換により（ノイズを含む）信号を回転させる。すると、適切なフィルタを適用することにより欲しい信号のみを通すことができる。したがってノイズは完全に除去される。その後さらに分数次フーリエ変換を適用することにより信号を元にもどせば欲しかった信号が得られる。

分数次フーリエ変換は光学系の設計やホログラフィックストレージの効率最適化に用いられることもある。

したがって、時間領域における打ち切り、もしくは同じことだが周波数領域におけるローパスフィルターの適用により、時間・周波数領域の任意の凸包を切り取ることができる。対して、分数次フーリエ変換を使わず時間領域的手法や周波数領域的手法のみを用いる場合、それらの軸に平衡な矩形を切り取ることしかできない。

関連項目

• 分数階微積分学
• メーラー核

その他の時間・周波数変換:

• 線形正準変換
• 短時間フーリエ変換
• ウェーブレット変換
• チャープレット変換
• 錐型分布関数

出典

外部リンク

• DiscreteTFDs -- software for computing the fractional Fourier transform and time-frequency distributions
• "Fractional Fourier Transform" by Enrique Zeleny, The Wolfram Demonstrations Project.
• Dr YangQuan Chen's FRFT (Fractional Fourier Transform) Webpages
• LTFAT - A free (GPL) Matlab / Octave toolbox Contains several version of the fractional Fourier transform.

参考文献

• Ozaktas, Haldun M.; Zalevsky, Zeev; Kutay, M. Alper (2001), The Fractional Fourier Transform with Applications in Optics and Signal Processing, Series in Pure and Applied Optics, John Wiley & Sons, ISBN 0-471-96346-1, http://www.ee.bilkent.edu.tr/~haldun/wileybook.html 
• Candan, C.; Kutay, M.A.; Ozaktas, H.M. (May 2000), “The discrete fractional Fourier transform”, IEEE Transactions on Signal Processing 48 (5): 1329–1337, doi:10.1109/78.839980 
• Lohmann, Adolf W. (Oct 1993). = josaa-10-10-2181 “Image rotation, Wigner rotation, and the fractional Fourier transform”. J. Opt. Soc. Am. A 10 (10): 2181–2186. doi:10.1364/JOSAA.10.002181. http://josaa.osa.org/abstract.cfm?URI = josaa-10-10-2181. 
• Pei, Soo-Chang; Ding, Jian-Jiun (Aug 2001). “Relations between fractional operations and time-frequency distributions, and their applications”. IEEE Transactions on Signal Processing 49 (8): 1638–1655. doi:10.1109/78.934134. ISSN 1053-587X. 
• Jian-Jiun Ding, Time frequency analysis and wavelet transform class notes, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2007.
• Saxena, Rajiv; Singh, Kulbir (Jan.–Feb. 2005). “Fractional Fourier transform: A novel tool for signal processing”. J. Indian Inst. Sci. 85 (1): 11–26. http://journal.library.iisc.ernet.in/index.php/iisc/article/view/2395.